Causal Bounds for Experimental Data
Causal Question
What are the bounds on the Individual Treatment Effect (ITE) of smoking 🚬 vs. not smoking 🚭 on COPD 🫁, given an Experimental Data?
These kind of experiments are considered to be non-ethical, yet even if they were - we can’t tell for sure what is the proportion of the Responders in the population.
Fortunately we can use Fréchet Inequalities for Causal Bounds.
😇 God-Given Counterfactual Data
- By God-Given knowledge we have access to the true counterfactual outcomes for each individual for smoking 🚬 and for not smoking 🚭
😇 God-Given Counterfactual Data
By God-Given knowledge we have access to the true counterfactual outcomes for each individual for smoking 🚬 and for not smoking 🚭
This gives us 4 Responders: people who get COPD only if they smoke, and avoid it otherwise. It also goes by the name PNS: Probability of Necessity and Sufficiensy:
\(\text{PNS} = \frac{4}{16} = 0.25\)
🦹 Evil RCT for Counterfactual Estimation
By God-Given knowledge we have access to the true counterfactual outcomes for each individual for smoking 🚬 and for not smoking 🚭
This gives us 4 Responders: people who get COPD only if they smoke, and avoid it otherwise. It also goes by the name PNS: Probability of Necessity and Sufficiensy:
\(\text{PNS} = \frac{4}{16} = 0.25\)
- In order to estimate the Average-Treatment-Effect an evil researcher forced a Randomized Controlled Trial.
🦹 Evil RCT for Counterfactual Estimation
By God-Given knowledge we have access to the true counterfactual outcomes for each individual for smoking 🚬 and for not smoking 🚭
This gives us 4 Responders: people who get COPD only if they smoke, and avoid it otherwise. It also goes by the name PNS: Probability of Necessity and Sufficiensy:
\(\text{PNS} = \frac{4}{16} = 0.25\)
Control Arm 🚭
\[\small{\hat{p}(Y=1|do(A=0)} = \frac{4}{8}\]
Treatment Arm 🚬
\[\small{\hat{p}(Y=1|do(A=1))} = \frac{5}{8}\]
In order to estimate Causal Bounds for PNS we can use the Fréchet Inequalities:
Control Arm 🚭
\[\small{\hat{p}(Y=1|do(A=0)} = \frac{4}{8}\]
Treatment Arm 🚬
\[\small{\hat{p}(Y=1|do(A=1))} = \frac{5}{8}\]
In order to estimate Causal Bounds for PNS we can use the Fréchet Inequalities:
\[\small{\text{PNS} = {\hat{p}(Y=1|do(A=1) , Y=0|do(A=0))} \leq min(\hat{p}(Y=1|do(A=1),\hat{p}(Y=0|do(A=0))))}\] \[\small{\text{PNS} = {\hat{p}(Y=1|do(A=1) , Y=0|do(A=0))} \geq \hat{p}(Y=1|do(A=1)) - \hat{p}(Y=1|do(A=0))}\]
Control Arm 🚭
\[\small{\hat{p}(Y=1|do(A=0)} = \frac{4}{8}\]
Treatment Arm 🚬
\[\small{\hat{p}(Y=1|do(A=1))} = \frac{5}{8}\]
In order to estimate Causal Bounds for PNS we can use the Fréchet Inequalities:
\[\small{\text{PNS} \leq min(\frac{4}{8},\frac{5}{8})}\] \[\small{\text{PNS} \geq \frac{5}{8} - \frac{4}{8}}\]
Control Arm 🚭
\[\small{\hat{p}(Y=1|do(A=0)} = \frac{4}{8}\]
Treatment Arm 🚬
\[\small{\hat{p}(Y=1|do(A=1))} = \frac{5}{8}\]
In order to estimate Causal Bounds for PNS we can use the Fréchet Inequalities:
\[\frac{1}{8} \leq\text{PNS} = \frac{4}{16} \leq \frac{4}{8}\]
The result resonates with the true god-given PNS!
Monotonicity: From Bounds to Point-Estimate
4 Types of Patients, or is it 3?
- The ITE on this example is being declared in harmful values - positive ITE means a harmful effect.
4 Types of Patients, or is it 3?
The ITE on this example is being declared in harmful values - positive ITE means a harmful effect.
Is it reasonable to allow positive effect of cigarettes in our analysis? Let’s consider the bounds with no Beneficiers allowed.
Control Arm 🚭
\[\small{\hat{p}(Y=1|do(A=0)} = \frac{4}{8}\]
Treatment Arm 🚬
\[\small{\hat{p}(Y=1|do(A=1))} = \frac{5}{8}\]
\[\small{\hat{p}(Y=1|do(A=0))} = \small{\hat{p}(\text{Lost-Causes}))} = \frac{4}{8}\] \[\small{\hat{p}(Y=0|do(A=1))} = \small{\hat{p}(\text{Immuned}))} = \frac{3}{8}\] \[\small{\text{PNS}} = {\hat{p}(\text{Responder})} = max(0, 1 - \frac{3}{8} - \frac{4}{8}) = \frac{1}{8}\]
🦹 Evil RCT with Time Machine
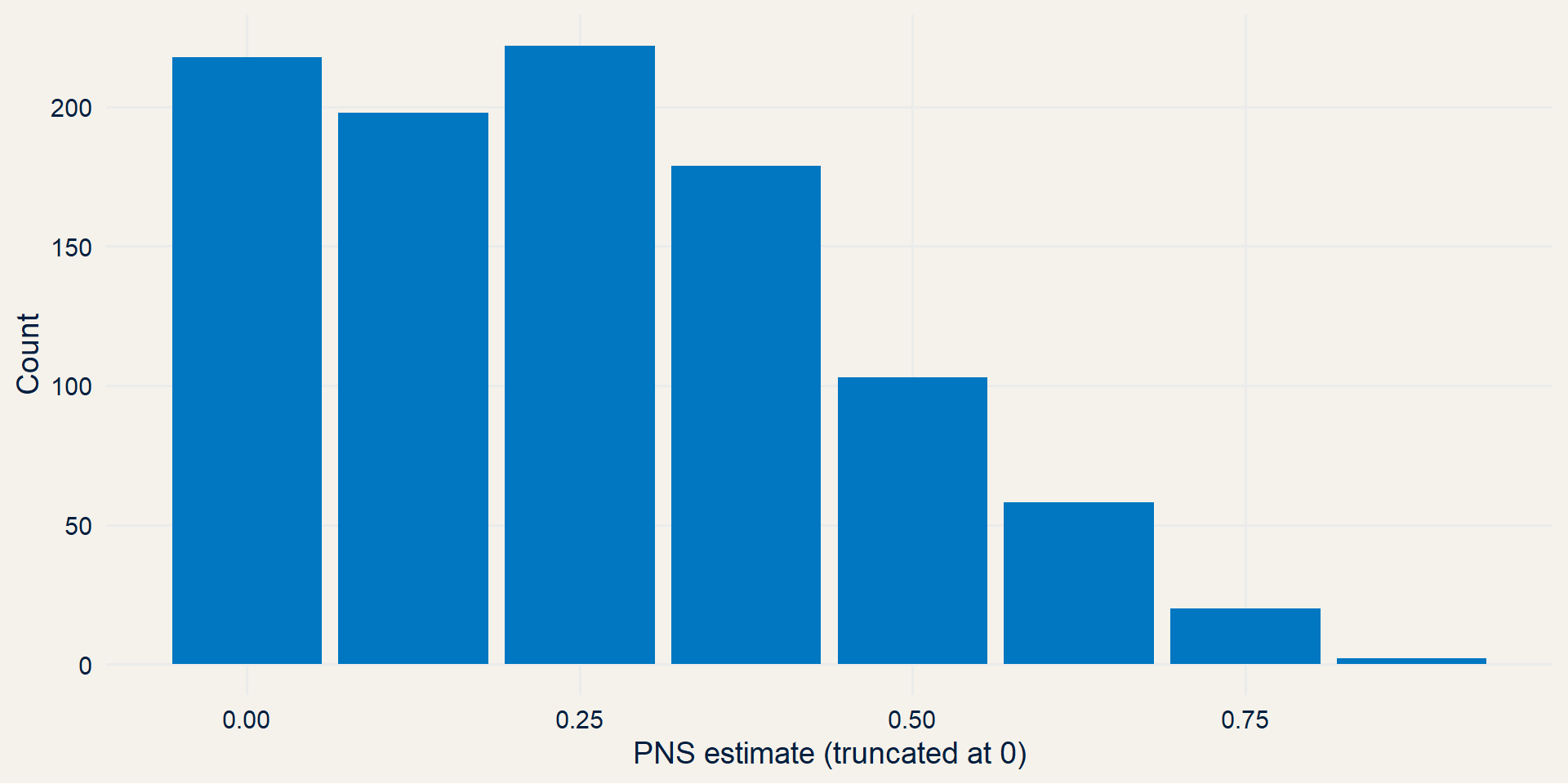
Our supervillain didn’t trust the estimated PNS=1/8, so he decided to use a Time-Machine and re-randomize the patients for treatment and control over and over again.
As can be seen from his histogram, the most frequent estimate is equal to the true God-Given PNS = 4/16 = 0.25.
